算法排序之快速、希尔、堆排序

快速排序法

  • 思想是每次选取一个数，将它移动到数组之间，使其左边全部都是比它小的数，它的右边都是比它大的数
  • 数组中选取一个数，与左边第一个数进行交换，从第二个数开始逐步排序(比它大的位置就不动，比它小的就换到前面，这样大的数也就自动的移动到了后面)，最后在将第一个数与比它小的最后一个数进行交换使其移动到数组中间，使得左边的数都小于它，右边的数都大于它

​

存在问题

对于选取的数是左边第二个，如果是完全有序的数组，则每次递归左边都是nil，右边是比原先数组少一个元素的数组，即会递归n次
此时时间复杂度为n²，而栈的深度也会为n，会导致栈溢出的情况

​

解决方法

  • 在partition时选取[l,r]之间的随机数，防止是有序数组而导致算法性能退化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func sortQuick(arr []int) {
   QuickSort(arr, 0, len(arr)-1)
}

func QuickSort(arr []int, l, r int) {
   if l >= r {
      return
   }
   p := partition(arr, l, r)
   QuickSort(arr, l, p-1)
   QuickSort(arr, p+1, r)
}

//就是使[l+1,j]<v,[j+1,i]>v
func partition(arr []int, l, r int) int {
   //生成[l,r]之间的随机索引，防止是有序数组而导致算法性能退化
   rand.Seed(time.Now().UnixNano()) 
   v := rand.Intn(r-l+1) + l
   arr[v], arr[l] = arr[l], arr[v] //将其随机的数作为数组的一个元素

   j := l //指向比v小的最后一个元素
   for i := l + 1; i <= r; i++ {
      if arr[i] < arr[l] {
         j++                             //加了1后指向比v大的第一个元素
         arr[i], arr[j] = arr[j], arr[i] //等于将这个数插入到比v小的数组的到最后一个
      }
   }
   arr[l], arr[j] = arr[j], arr[l] //因为j是指向比v小的最后一个元素，这次交换将v变成了左边都比v小右边都比v大
   return j
}

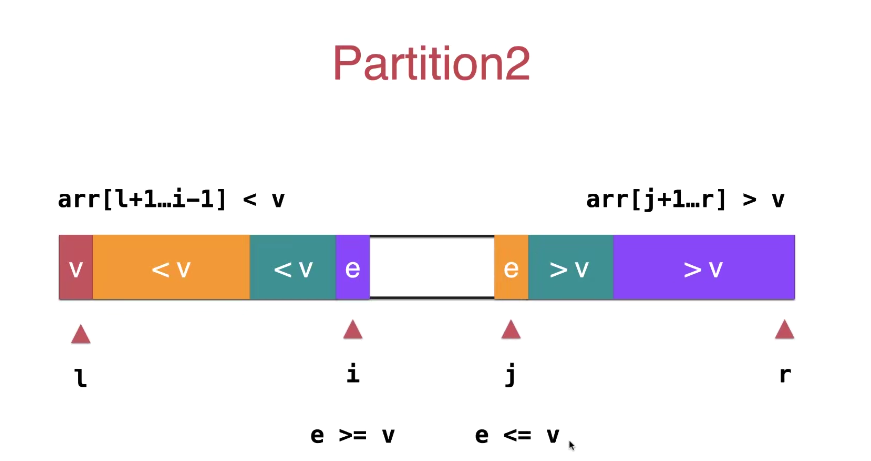
双路快速排序法

存在问题

即使加入了随机数，但是在一个所有数相等的数组中，快速排序法还是退化成了n²的复杂度

​

解决思路

  • 使用双路快速排序法 目的是将数组元素尽可能的分散在标定元素两侧
    目的是使得 arr[l+1,i-1]<=v** **arr[j+1,r]>=v

image-20210319192152777

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//快速排序法还是存在问题，即如果对于完全相同的一组数，还是会将其分成一边为空一边少一个元素
func partition2(arr []int, l, r int) int {
   //生成[l,r]之间的随机索引，防止是有序数组而导致算法性能退化
   rand.Seed(time.Now().UnixNano()) 
   v := rand.Intn(r-l+1) + l
   arr[v], arr[l] = arr[l], arr[v] //将其随机的数作为数组的一个元素

   //arr[l+1,i-1]<=v arr[j+1,r]>=v
   i := l + 1
   j := r
   for ; ; {
      for ; i <= j && arr[i] < arr[l]; {
         i++
      }
      for ; i <= j && arr[j] > arr[l]; {
         j--
      }
      if i >= j {
         break
      }
      //当i遇到比l大的元素就停下，j遇上比l小的元素就停下，进行交换，使得arr[l+1,i-1]<=v arr[j+1,r]>=v
      arr[i], arr[j] = arr[j], arr[i]
      i++
      j--
   }
   arr[l], arr[j] = arr[j], arr[l] //此时只能用j替换和返回而不能是i，因为如果当i和j进到相同位置时此而时该数又比v小则会出错（将大的数交换到l位置了）
   return j
}

复杂度

由于加入了随机数和双路排序思想，则不能找到一个100%恶化的数组

则此时双路快速排序法是一个随机算法，不能采用最差情况讨论复杂度，而是要看期望

其期望还是 nlogn 的复杂度

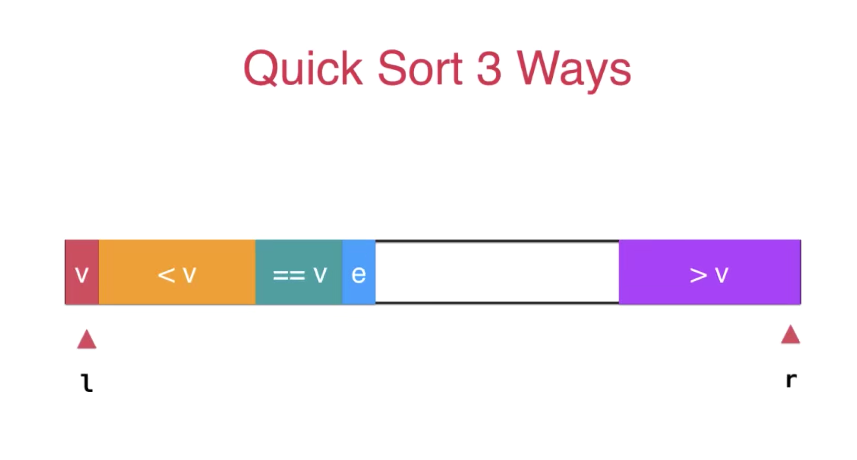
三路快速排序法

存在问题

在二路快排中，虽然相同元素的数组中的元素被均摊到了两边，但是可以不必要再对相同元素再进行排序

​

解决思路

  • 对于元素一样的数组，其复杂度为 n

​ 目的是使得 arr[l+1,lt]<v** **arr[lt+1,i-1]=v** **arr[gt,r]>v

image-20210319192236771

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func QuickSort3way(arr []int, l, r int) {
   if l >= r {
      return
   }
   v := rand.Intn(r-l+1) + l
   arr[v], arr[l] = arr[l], arr[v]
   //arr[l+1,lt]<v arr[lt+1,i-1]=v arr[gt,r]>v
   //lt指向小于v的最后一个元素，gt指向大于v的第一个元素
   lt := l
   i := l + 1
   gt := r + 1
   for ; i < gt; {
      if arr[i] < arr[l] {
         lt++
         arr[lt], arr[i] = arr[i], arr[lt]
         i++
      } else if arr[i] > arr[l] {
         gt--
         arr[gt], arr[i] = arr[i], arr[gt] //此时不用i++，因为此时来了一个新的元素arr[gt]，这个元素还没有比较
      } else {
         i++
      }
   }
   arr[l], arr[lt] = arr[lt], arr[l]
   //arr[l,lt-1]<v arr[lt,gt-1]==v arr[gt,r]>v
   QuickSort3way(arr, l, lt-1)
   QuickSort3way(arr, gt, r)
}

堆排序法

将数组中的数加入堆复杂度是 nlogn

将堆中依次 ExtractMax 复杂度是 nlogn

总复杂度是 2nlogn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
func HeapSort(arr []int) {
   h := heap.NewMaxHeap(len(arr))
   //nlogn
   for _, v := range arr {
      h.Add(v)
   }
   //nlogn
   for i := len(arr) - 1; i >= 0; i-- {
      arr[i] = h.ExtractMax()
   }
}

//取出元素 取出最大的元素 就是删除头结点
func (h *MaxHeap) ExtractMax() int {
	res := h.FindMax()
	//将尾结点和头结点交换，再删除尾结点，相当于删除了头结点
	h.Array.Swap(0, h.Array.Length-1)
	h.Array.RemoveLast()
	//但是此时不满足完全二叉树的性质，需要进一步整理
	h.shiftDown(0)
	return res
}

//从头结点就是，找出自己左右孩子中最大的值，如果自己比它小，则进行交换
func (h *MaxHeap) shiftDown(k int) {
	for leftChild(k) < h.Array.GetSize() { //判断左孩子是否存在
		j := leftChild(k)
		if j+1 < h.Array.GetSize() && h.Array.Get(j) < h.Array.Get(j+1) { //j+1就是右孩子
			j = rightChild(k)
		}
		//此时data[j]就是左右孩子中最大的值
		if h.Array.Get(j) <= h.Array.Get(k) {
			break
		}
		h.Array.Swap(k, j)
		k = j
	}
}

优化

通过Heapify将数组堆化，其时间复杂度是 n

没有开辟额外空间，空间复杂度是 1

思路是：

  • 将堆化的数组第一个元素和最后一个元素进行交换，使得最后一个元素排序成功
  • 此时前n-1个元素又不满足最大堆，则通过特殊的shiftDown将前n-1个元素排序成堆
  • 此时再将第一个元素和倒数第二个元素进行交换，直至排序成功
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func HeapSort2(arr []int) {
   if len(arr) <= 1 {
      return
   }
   heap.Heapify(arr)
   for i := len(arr) - 1; i >= 0; i-- {
      arr[0], arr[i] = arr[i], arr[0]
      shiftDownArr(arr, 0, i)
   }
}

//将任意数组转化成成堆形式
//只需拿到最后一个非叶子结点，依次向前shiftDown (抛弃掉了所有叶子结点，相当于少了一半)
//最后一个非叶子结点只需要最后一个结点再求它的parent
//其复杂度是n
func Heapify(arr []int) {
	h := MaxHeap{*array.NewInArray(arr, len(arr))}
	for i := parent(len(arr) - 1); i >= 0; i-- {
		h.shiftDown(i)
	}
}

func shiftDownArr(arr []int, k, n int) {
   for 2*k+1 < n {
      j := 2*k + 1 //左孩子索引
      if j+1 < n && arr[j] < arr[j+1] {
         j++ //j等于右孩子索引
      }
      if arr[j] <= arr[k] {
         break
      }
      arr[k], arr[j] = arr[j], arr[k]
      k = j
   }
}

希尔排序法

  • 基本思想：让数组越来越有序，不能只处理相邻逆序对

对元素间距为n/2的所有数组做插入排序，对元素间距为n/4的所有数组做插入排序， … 对元素间距为1进行插入排序

看上去有四重循环，实际上其因为数组会越来越有序，循环n的次数也会越来越少，其复杂度是大于nlogn而小于n²，在数组小的时候其性能可能还会超越nlogn
并且没有使用递归，仅依靠循环就完成了排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func ShellSort(arr []int) {
	h := len(arr) / 2
	for h >= 1 {
		for start := 0; start < h; start++ {
			//对data[start,start+h,start+2h...]进行插入排序
			for i := start + h; i < len(arr); i += h {
				//使用插入排序法
				for j := i; j-h >= 0 && arr[j] < arr[j-h]; j -= h {
					arr[j], arr[j-h] = arr[j-h], arr[j]
				}
			}
		}
		h /= 2
	}
}

优化

四重循环压缩成三重循环，但是复杂度并没有改变
不用分别对分开的数组对分别使用插入排序,可以直接交替对数组对使用插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
func ShellSort2(arr []int) {
	h := len(arr) / 2
	for h >= 1 {
		//对data[h...]进行插入排序
		for i := h; i < len(arr); i++ {
			//使用插入排序法
			for j := i; j-h >= 0 && arr[j] < arr[j-h]; j -= h {
				arr[j], arr[j-h] = arr[j-h], arr[j]
			}
		}
		h /= 2
	}
}

步长序列

步长序列不同，复杂度分析不同，因为步长序列是一个超参数

还没有证明出一个最好的步长序列使得希尔排序性能最好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func ShellSort3(arr []int) {
	h := 0
	for h < len(arr) {
		h = 3*h + 1
	}
	for h >= 1 {
		//对data[h...]进行插入排序
		for i := h; i < len(arr); i++ {
			//使用插入排序法
			for j := i; j-h >= 0 && arr[j] < arr[j-h]; j -= h {
				arr[j], arr[j-h] = arr[j-h], arr[j]
			}
		}
		h /= 3
	}
}

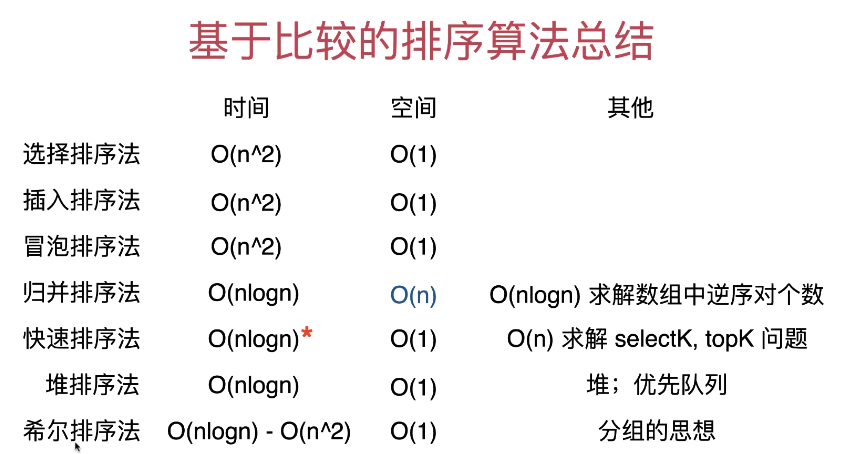
基于比较的排序算法总结

时空复杂度

image-20210329114121325

快速排序法是一个随机算法，则时间复杂度要用期望

​

image-20210329114302831

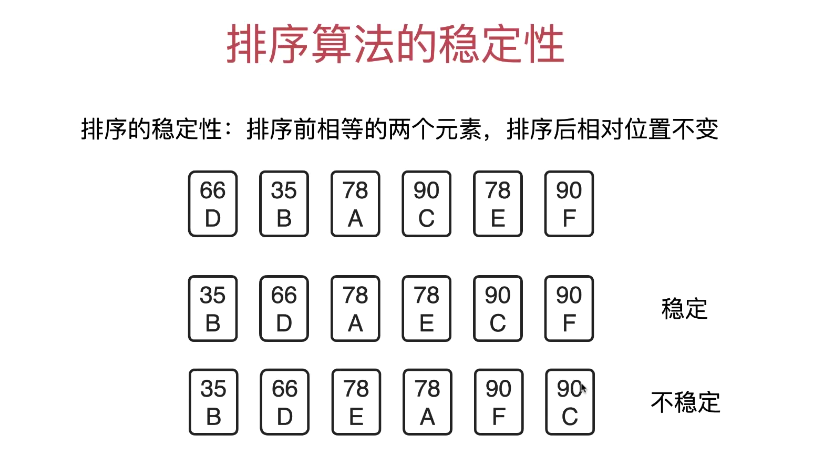
稳定性

如果元素只有一个域，稳定性没有意义

image-20210329114839253

​

基础排序算法的稳定性

插入排序法中相同的元素没有机会进行 “跳跃“

image-20210329124619316

​

高级排序算法的稳定性

image-20210329125243456

Golang 排序

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！